Inventory Management with Attention-Based Meta Actions

泉谷 圭亮，シモセラ エドガー

ローグライクゲームは強化学習アルゴリズムにとって非常に挑戦的な環境である．というのも，ゲームに敗北する度に最初からやり直さなければならず，環境は確率的かつ手続き的に生成され，そして適切にゲーム内のアイテムを使用することがゲーム攻略には不可欠であるためである．最近の研究では，ローグライクを基にした強化学習アルゴリズムのための環境や，挑戦的なローグライクに取り組むモデルが提案されているが，我々の調査する限り，アイテムの扱いを対象としたものはない．アイテムはゲーム中に得られるもので，ローグライクにおいて重要な役割を果たしている．しかし，アイテムは数が可変の非順序集合であり，さらにそれらが行動空間の一部を構成しているため，強化学習フレームワークにアイテムを組み込むのは簡単ではない．本研究では，非順序集合が行動空間の一部となっているこの問題に取り組み，アイテムを用いた行動も扱えるattentionベースの機構と，複雑な行動やアイテムを扱えるメタ行動フレームワークとを提案する．これらを挑戦的なゲームであるNetHackで評価した結果，提案手法は既存手法を大幅に上回る性能を示した．

口頭発表

モデル

既存のモデル（破線の上側）に対して，行動再帰とアイテム特徴抽出とを組み込んでいる．

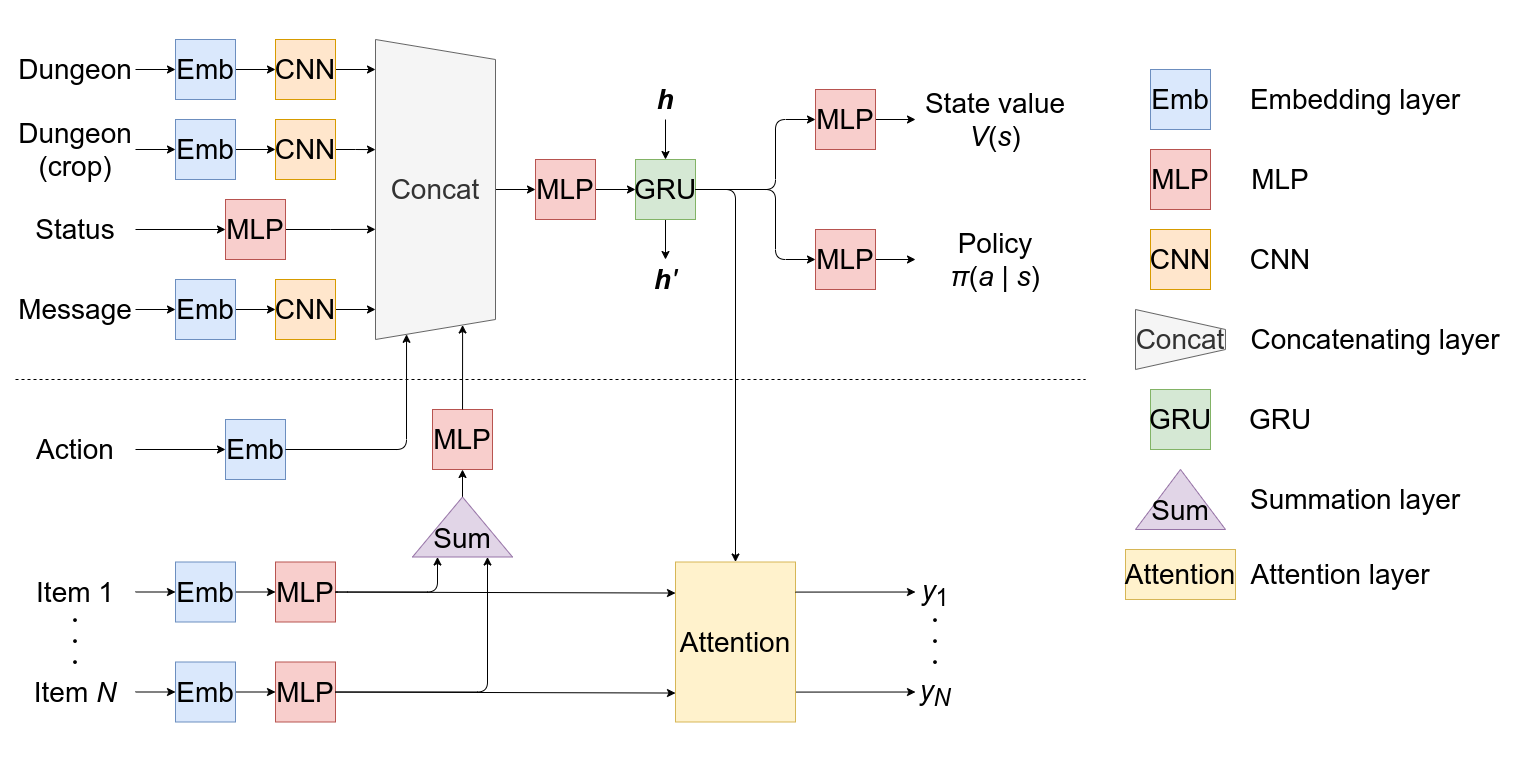
行動再帰

直前に取った行動を現在の状態の表現に組み込むため，埋め込み層をモデルに追加する．

インベントリの特徴抽出

所持している各アイテムの特徴 xi\bm{x_i} を計算した後，全アイテムの特徴 x\bm{x} を， 順序に依らない演算 x=MLP(∑ixi)\bm{x}=\mathrm{MLP}\left(\sum_i{\bm{x_i}}\right) により計算する．

アイテムのスコア計算

行動決定時に用いる各アイテムのスコアをattention機構を用いて計算する． 具体的には，行列 WQ,WK\bm{W_Q}, \bm{W_K} とベクトル wV\bm{w_V} を用いて，ii 番目のアイテムのスコア yiy_i を

yi=q⊤kidkviy_i=\frac{\bm{q}^{\top}\bm{k_i}}{\sqrt{d_k}}v_i

によって計算する．ここで，

q=WQf,ki=WKxi,vi=wV⊤xi\begin{aligned} \bm{q} &= \bm{W_Q}\bm{f}, \\ \bm{k_i} &= \bm{W_K}\bm{x_i}, \\ v_i &= \bm{w_V}^{\top}\bm{x_i} \end{aligned}

であり，dkd_k は q\bm{q} や ki\bm{k_i} の次元，f\bm{f} は現在の状態の表現（GRUの出力）である．

正誤表

ページ場所誤正
5式(9) 2行目+λπv(b0∣St)∇∑b∈Ai−πi(b∣St)log⁡πi(b∣St){}+\lambda\pi_{\mathrm{v}}(b_0\mid S_t)\nabla\sum_{b\in\mathcal{A}_{\mathrm{i}}}-\pi_{\mathrm{i}}(b\mid S_t)\log\pi_{\mathrm{i}}(b\mid S_t)+λ∇πv(b0∣St)∑b∈Ai−πi(b∣St)log⁡πi(b∣St){}+\lambda\nabla\pi_{\mathrm{v}}(b_0\mid S_t)\sum_{b\in\mathcal{A}_{\mathrm{i}}}-\pi_{\mathrm{i}}(b\mid S_t)\log\pi_{\mathrm{i}}(b\mid S_t)